Notions ensemblistes

Un ensemble est un objet mathématique qui formalise la notion de contenant sans ordre ni répétition. Par exemple, une classe est un ensemble d’élèves, que l’on peut certes ordonner selon la taille, l’âge, le nom de famille ou la moyenne de mathématiques, mais qui reste la même classe indépendamment de ces ordres.

Le fait qu’un ensemble E contienne un élément x se note x ∈ E et on dit alors que x appartient à E. Dans le cas contraire, on note x ∉ E.

Un ensemble peut contenir n’importe quel objet mathématique, y compris des listes ou d’autres ensembles.

Exemples fondamentaux

Liste exhaustive

La description la plus élémentaire d’un ensemble consiste à lister ses éléments entre accolades. Ni l’ordre d’énonciation ni les éventuelles répétitions dans la liste n’ont d’influence sur l’ensemble ainsi décrit : {∗ ; ∘} = {∘ ; ∗} = {∗ ; ∗ ; ∘ ; ∗ ; ∘}. En effet, les ensembles sont caractérisés par les éléments qu’ils contiennent, c’est-à-dire que deux ensembles sont égaux si et seulement s’ils contiennent les mêmes objets.

L’ensemble vide est le seul ensemble qui ne contient aucun élément et il se note ∅.

Attention, la description par liste n’est plus envisageable pour des ensembles qui contiennent un trop grand nombre d’éléments, et a fortiori pour les ensembles infinis.

Exercice

Lister les différents éléments de l’ensemble {∘ ; (∘ ; ∗) ; {∗ ; ∘} ; {∘} ; (∘ ; ∘) ; {∘ ; ∘} ; {∘ ; ∗}}.

Ne pas confondre un nombre avec l’ensemble qui contient ce nombre. Ne pas confondre une liste avec l’ensemble des éléments d’une liste. Pour un ensemble, l’ordre d’énonciation et les répétitions sont sans importance.

Ensembles de nombres

On définit plusieurs ensembles de nombres standards :

l’ensemble N des entiers naturels (0, 1, 2, 3, …)
l’ensemble Z des entiers relatifs, qui contient tous les naturels et leurs opposés (0, 1, −1, 2, −2, …)
l’ensemble D des nombres décimaux positifs ou négatifs, c’est-à-dire les entiers et les nombres dits « à virgule »
l’ensemble Q des nombres rationnels, qui peuvent s’écrire comme une fraction d’entiers (0, −3/2, 1/3, …), ce qui comprend en particulier tous les décimaux
l’ensemble R des nombres réels qui peuvent être décrits par un développement décimal fini ou infini, comprenant les rationnels et d’autres nombres tels que π et √(2), et qui permettent de repérer les points d’un axe orienté
l’ensemble C des nombres complexes, s’écrivant sous la forme a + bi où i est l’unité imaginaire avec a et b deux réels quelconques, et qui permettent de repérer tous les points du plan.

Pour éviter de confondre les notations de ces ensembles avec des variables, on les écrit de façon manuscrite avec une double barre.

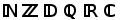
Chacun de ces ensembles peut être caractérisé par certaines propriétés qui définissent notamment sa structure : Z et D sont des groupes abéliens (et même des anneaux) tandis que Q, R et C sont des corps commutatifs.

Ces ensembles sont construits par divers procédés. L’ensemble des entiers naturels se déduit de l’axiome de l’infini selon un procédé dû à Von Neumann. L’ensemble des entiers relatifs est une symétrisation de N, tandis que l’ensemble des rationnels est le corps des fractions associé. L’ensemble des réels peut s’obtenir de façon naïve par des séries de décimales, mais a été introduit historiquement par les coupures de Dedekind et, de façon plus moderne, comme classes de suites de Cauchy à valeurs rationnelles. Enfin, les nombres complexes peuvent être vus entre autres comme des points du plan R², des matrices de similitude ou encore des classes de polynômes.

Constructions

Produit cartésien

Si E et F sont deux ensembles (éventuellement identiques), leur produit cartésien, noté E×F (qui se lit « E croix F »), est l’ensemble des couples de premier terme dans E et de deuxième terme dans F.

Exemple

{0 ; 2} × {1 ; 2 ; 3} = {(0 ; 1), (0 ; 2), (0 ; 3), (2 ; 1), (2 ; 2), (2 ; 3)}

Si E ≠ F et que ces deux ensembles sont non vides, alors on a E × F ≠ F × E.

Exercice

Comparer {0 ; 2} × {1 ; 2 ; 3} et {1 ; 2 ; 3} × {0 ; 2}.

Cette construction permet de décrire des ensembles comme un jeu de 32 cartes : chaque carte est identifiée par une valeur et une enseigne (ou couleur) et tous les couples sont représentés, d’où l’écriture {7, 8, 9, 10, V, D, R, A} × {♠, ♥, ♦, ♣}.

On peut noter aussi E² = E × E, l’ensemble des couples d’éléments de E, puis E³ = E × E × E et ainsi de suite. L’ensemble des résultats possibles de deux lancers successifs d’un dé standard à six faces peut être représenté par {1 ; 2 ; 3 ; 4 ; 5 ; 6}².

Exercice

Représenter l’ensemble des résultats possibles de trois lancers successifs d’une pièce à pile ou face, sous forme d’un produit cartésien puis à l’aide d’une liste exhaustive.

Plus généralement, on peut définir le produit cartésien d’une liste d’ensembles, notamment pour énoncer des propriétés universelles.

Autres axiomes

On dispose des deux schémas d’axiomes suivants.

Compréhension: Étant donné un ensemble E et un prédicat P dépendant d’une variable, c’est-à-dire une formule pouvant être vraie ou fausse selon la valeur de la variable, l’ensemble {x ∈ E : P(x)} = {x ∈ E / P(x)} est l’ensemble des éléments de E qui satisfont la formule (éventuellement aucun ou tous).
Remplacement: Étant donné un ensemble E et une formule F dépendant d’une variable, l’ensemble {F(x), x ∈ E} est l’ensemble des objets construits à partir de la formule F sur les éléments de E.

Par exemple, on peut définir ⟦1 ; 6⟧ = {k ∈ N : 1 ≤ k ≤ 6}, R^∗ = {x ∈ R : x ≠ 0}, Z = {a − b, (a, b) ∈ N²} et Q = {p/q, (p, q) ∈ Z × N*}.

Définition

Pour tout (a, b) ∈ N² tel que a ≤ b, on pose ⟦a, b⟧ = {k ∈ N : a ≤ k ≤ b}.

Exercice

Décrire chacun des ensembles suivants à l’aide d’une liste exhaustive :

{(k − 7/2)², k ∈ ⟦1 ; 6⟧}
{x ∈ R^∗ : x = 1 + 1/x}
{x ∈ Q : x² = 2}
{(−1)ⁿ, n ∈ N}
{k ∈ ⟦1 ; 6⟧ : k est pair}
{k est pair, k ∈ ⟦1 ; 6⟧}

Parties

Relation d’inclusion et ensemble des parties

Il ne faut pas confondre la relation d’appartenance avec la relation d’inclusion : on dit qu’un ensemble A est inclus dans un ensemble E et on note A ⊂ E si tous les éléments de A sont aussi éléments de E. En particulier, l’ensemble vide est inclus dans tous les autres ensembles.

On obtient aussi la suite d’inclusions d’ensembles de nombres : N ⊂ Z ⊂ D ⊂ Q ⊂ R ⊂ C.

La relation d’inclusion satisfait les propriétés suivantes.

Réflexivité: Tout ensemble est inclus dans lui-même.
Antisymétrie: Deux ensembles sont égaux si et seulement s’ils sont mutuellement inclus l’un dans l’autre : E = F ⇔ (E ⊂ F et F ⊂ E).
Transitivité: Si un ensemble est inclus dans un deuxième qui est inclus dans un troisième alors le premier est inclus dans le troisième : (E ⊂ F et F ⊂ G) ⇒ E ⊂ G.

Exercice

Vérifier que la relation d’inclusion n’est pas totale.

Définition

Si E est un ensemble, les parties de E sont les ensembles inclus dans E et on note 𝒫(E) l’ensemble des parties de E.

Exercice

Expliciter les ensembles 𝒫({1 ; 2}), 𝒫(∅) et 𝒫(𝒫(∅)).

Opérations ensemblistes

Définition

Si A et B sont deux parties d’un ensemble E, on définit leur intersection A ∩ B = {x ∈ E : x ∈ A et x ∈ B}, leur réunion A ∪ B = {x ∈ E : x ∈ A ou x ∈ B}.

Propriété

L’union et l’intersection sont deux opérations associatives, commutatives et distributives chacune par rapport à l’autre.

Définition

Si A est une partie d’un ensemble E, le complémentaire de A dans E est l’ensemble E ∖ A = {x ∈ E : x ∉ A}.

Lorsqu’il n’y a pas d’ambiguïté sur l’ensemble englobant, le complémentaire d’une partie A peut aussi se noter avec une barre suscrite A‾, notamment en théorie des probabilités.

Lois de De Morgan: Si A et B sont deux parties d’un ensemble E, alors on a (A ∩ B)‾ = A‾ ∪ B‾ et (A ∪ B)‾ = A‾ ∩ B‾.

Définition

Deux ensembles sont dits disjoints si leur intersection est vide.

Exercice

Soient A et B deux parties d’un ensemble E. Montrer que A et B sont disjoints si et seulement si A‾ ∪ B‾ = E.

Définition

Une partition d’un ensemble E non vide est un ensemble de parties non vides de E, deux à deux disjointes et dont la réunion est égale à E.