Utilité combinée avec argsh

La fonction argument sinus hyperbolique (notée argsh en français, ou arcsinh en anglais) est parfois employée en économétrie comme fonction dérivable et croissante sur R tout en étant équivalente à la fonction logarithme en +∞. Elle permet ainsi d’atténuer l’effet marginal d’une grandeur tout en gardant un comportement linéaire au voisinage de 0. Cet article analyse l’utilisation de cette fonction pour l’évaluation de la mesure relative de deux grandeurs qui dépendent de façon affine d’un même paramètre réel.

Il est tentant de calculer alors la somme de ces deux grandeurs, ou une combinaison linéaire avec des coefficients à déterminer, mais le résultat reste une fonction affine du paramètre x. Dans ce cadre, seules les valeurs extrêmes du paramètre peuvent optimiser ce résultat, ce qui revient à complètement négliger une des deux grandeurs au profit de l’autre.

Une piste possible pour trouver une voie médiane consiste à atténuer l’effet marginal des grandeurs lorsqu’elles prennent des valeurs importantes, d’où l’idée d’une croissance logarithmique à l’infini, tout en préservant le caractère linéaire pour des valeurs faibles. On pose alors U = argsh(A) + argsh(B).

La fonction F : x ↦ argsh(ax + b) + argsh(cx + d) est dérivable avec pour tout x ∈ R, F′(x) = a/√((ax + b)² + 1) + c/√((cx + d)² + 1).

Comme on s’intéresse au cas où a et c sont de signes contraires, on suppose sans perte de généralité a > 0 > c, donc la dérivée ne s’annule que pour a√((cx + d)² + 1) = −c √((ax + b)² + 1)
⇔ a²((cx + d)² + 1) = c²((ax + b)² + 1)
⇔ a²(2cdx + d² + 1) = c²(2abx + b² + 1)
⇔ 2(a²cd − c²ab)x = c²(b² + 1) − a²(d² + 1)
⇔ (ad − bc)x = (c²(b² + 1) − a²(d² + 1))/2ac.

Pour peu qu’on ait ad − bc ≠ 0 (ce qui ressemble certes à la condition d’inversibilité d’une matrice 2×2, mais qui représente surtout ici le fait que les grandeurs A et B ne s’annulent pas pour la même valeur de x), on obtient donc un seul point critique de F en x^∗ = (c²(b² + 1) − a²(d² + 1))/(2ac(ad − bc)).

En outre, l’inéquation F′(x) > 0 se réécrit (ad − bc)x < (c²(b² + 1) − a²(d² + 1))/2ac (avec un changement de sens de l’inégalité à cause du signe de ac < 0) donc le point critique x^∗ correspond à un maximum si et seulement si ad − bc > 0.

Si les constantes b et d sont assez grandes en valeur absolue, on peut négliger les termes constants de valeur 1 pour aboutir à l’approximation adimensionnelle : x^∗ ≈ (c²b² − a²d²)/(2ac(ad − bc)) = (ad + bc)/−2ac = 1/2(−b/a + −d/c).

L’adimensionnalité signifie que cette formule est indépendante des choix d’unité respectifs pour les deux grandeurs.

Cette expression est exactement la moyenne arithmétique des points d’annulation des deux fonctions affines qui décrivent les grandeurs A et B. Elle correspond aussi à la valeur du paramètre qui maximise le produit AB. Cela s’explique par le fait que l’approximation revient à remplacer la fonction argsh par son équivalent ln en +∞, autrement dit on maximise ln(A) + ln(B) = ln(AB).

On peut se contenter de cette approximation si la positivité des deux grandeurs A et B est un prérequis absolu. Cependant, si les valeurs négatives sont admissibles pour l’une ou l’autre, la spécificité de la fonction argsh reste pertinente, et pose alors la question des unités choisies.

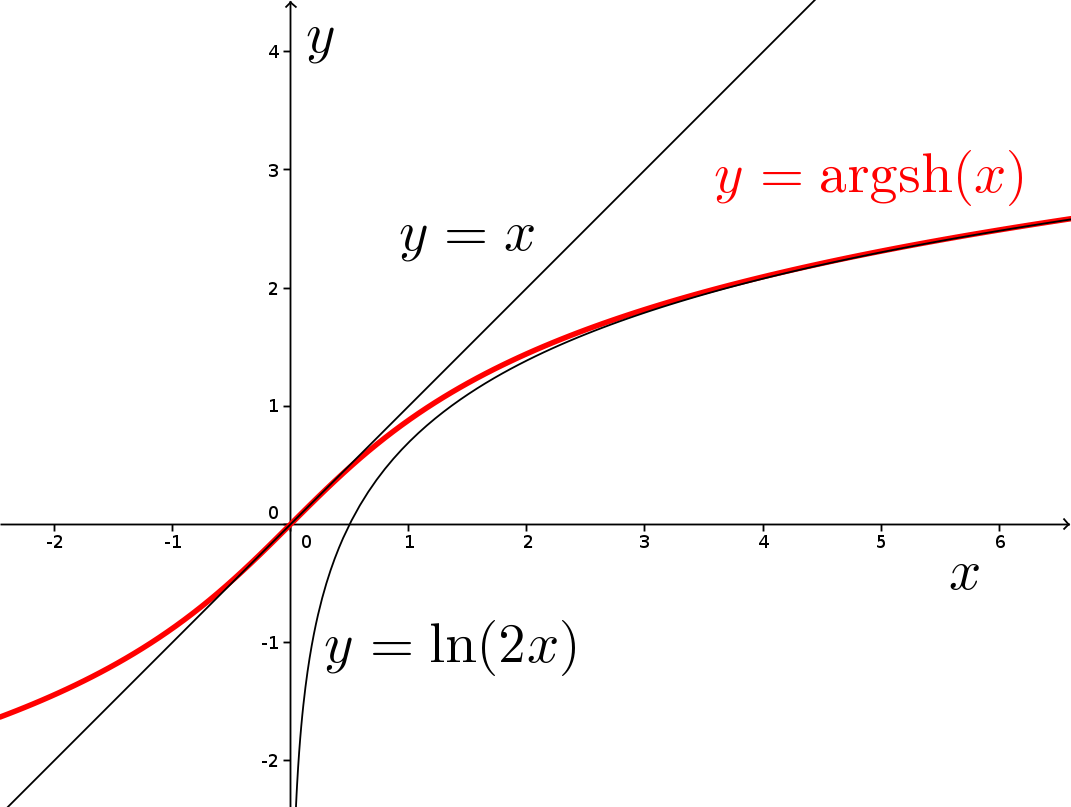
La fonction argsh est bien approchée par la fonction identité au voisinage de 0 (moins de 4 % d’écart en 0,5) et par la fonction x ↦ ln(2x) ensuite (moins de 4 % d’écart en 2). L’accroissement d’une unité au voisinage de 0 correspond donc à un doublement de la valeur ensuite. Il s’agit donc de choisir pour chaque grandeur une unité qui ait une valeur typique, par exemple un écart type de variations standard.

Si les deux grandeurs A et B n’ont pas été normalisées, on peut alors noter σ et τ leurs valeurs typiques respectives (éventuellement nulles pour des grandeurs qui ne peuvent avoir de valeurs négatives), et la déviation de l’approximation adimensionnelle s’écrit alors Δx = ((σc)² − (τa)²)/(2ac(ad − bc)).