Mon collègue Frédéric m’a demandé comment prouver, avec un maximum d’outils de terminale, qu’un objet mobile qui glisse sans frottement d’un point A à un point B (plus bas que A) ira plus vite s’il glisse sur une (demi-)cycloïde (qui passe par A et B) que s’il glisse sur un plan incliné rectiligne.
Description de la cycloïde
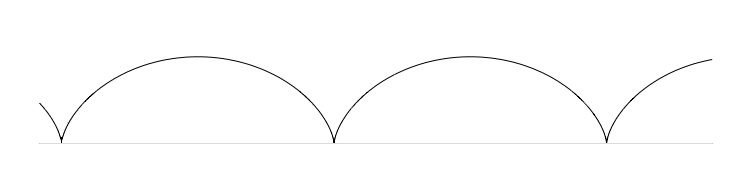
La cycloïde dont il est question est une courbe plane constituée d’une succession d’arches identiques mises bout à bout le long d’une droite. Chacune de ces arches ressemble à un demi-cercle allongé mais ce n’est pas un arc elliptique. La jonction entre deux arches successifs forme une pointe en contact perpendiculaire avec la droite.
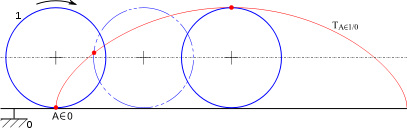
Le nom de cycloïde est lié au fait que cette courbe est celle que parcourt un point du bord d’une roue lorsque celle-ci roule sans glisser le long d’une chemin rectiligne. Le groupe LP TICE de l’IREM de Lyon propose une chronophotographie d’une valve de pneu qui permet de visualiser une trajectoire très proche de la cycloïde.
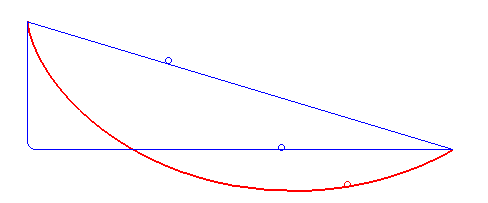
Parmi les nombreuses propriétés de la cycloïde, on trouve qu’elle donne la solution du problème de la brachistochrone (littéralement, « le temps le plus court »), c’est-à-dire de la courbe le long de laquelle un point matériel glisse sans frottement le plus rapidement possible entre deux points s’il est lâché sans vitesse initiale et dans un champ gravitationnel uniforme (ou n’importe quelle autre force, du moment qu’elle est constante le long de la trajectoire). La question peut paraitre curieuse, et la réponse encore plus, quand on se rappelle que le segment de droite est le plus court chemin entre ses extrémités. Mais il ne s’agit pas ici de parcourir le trajet à vitesse constante. Les forces extérieures et la réaction du support permettent de faire varier cette vitesse et d’éventuellement gagner du temps par rapport au trajet rectiligne.
Sans aller jusqu’à démontrer que cette courbe réalise le temps le plus court parmi toutes les courbes possibles, voici donc quelques calculs qui permettent de comparer les temps de trajet le long de la cycloïde et le long de la ligne droite.
Paramétrisation
Par définition de la mesure en radians, si la roue de rayon r tourne sans glisser d’un angle θ, elle avance d’une longueur rθ. En définissant l’origine du repère au point de contact initial de la roue avec la route, la route constituant l’axe des abscisses orienté dans le sens du déplacement, et la verticale étant l’axe des ordonnées orienté vers le haut, le centre de la roue après roulement d’un angle θ se retrouve donc au point de coordonnées (rθ, r), et un point au bord de la roue, initialement à l’origine du repère, se retrouve après roulement d’un angle θ au point de coordonnées (rθ − r sin(θ), r − r cos(θ)).
La courbe brachistochrone qui nous intéresse est en fait symétrique de celle-ci par rapport à l’axe des abscisses, un peu comme si la roue roulait sous la route au lieu de rouler dessus. On définit donc les coordonnées d’un point de cette courbe par x = r(θ − sin(θ)) et y = r(cos(θ) − 1). Le vecteur vitesse s’écrit donc v = (x′, y′) = rθ′(1 − cos(θ), − sin(θ)), et l’énergie cinétique du point (de masse m) vaut : 12m ‖v‖2 = mr2θ′2(1 − cos(θ)).
Cette énergie cinétique (nulle au point de départ) provient de l’énergie potentielle sous la forme −mgy = mgr(1 − cos(θ)) où g est l’intensité du champ de pesanteur (supposé uniforme dans l’espace donc constant le long de la trajectoire).
Par conservation de l’énergie totale, on obtient donc l’équation rθ′2 = g, d’où l’on tire que l’angle croît de façon linéaire : θ = √(gr)t, autrement dit qu’il se déplace le long de la courbe à la même vitesse que le point sur le bord de la roue.
Chute libre sur ligne inclinée
Si on relie l’origine du repère à un point de la cycloïde par un segment de droite d’équation y = −αx, un point matériel glissant sans frottement le long de ce segment a un vecteur vitesse qui s’écrit v = (x′, −αx′) donc l’énergie cinétique vaut 12m(1 + α2)x′2, et la conservation de l’énergie totale donne (1 + α2)x′2 = 2gαx, ce qui peut se réécrire x′2√x = √((gα)(2(1 + α2))), puis par intégration, √x = √((gα)(2(1 + α2)))t, ou encore t = √((2(1 + α2)x)(gα)) = √((2(x2 + y2))(gαx)).
Comparaison des deux temps de trajet
Pour montrer que ce temps est supérieur à celui obtenu par descente le long de la brachistochrone, il suffit de montrer l’inégalité
√((2(x2 + y2))(gαx))
≥ √(rg)θ
⇔ (2r2((θ − sin(θ))2 + (cos(θ) − 1)2))(gr(1 − cos(θ)))
≥ rgθ2
⇔ 2(θ2 − 2θ sin(θ) + 2 − 2 cos(θ))
≥ (1 − cos(θ))θ2
⇔ θ2(1 + cos(θ)) + 4(1 − θ sin(θ) − cos(θ)) ≥ 0.
On peut alors exprimer le membre de gauche comme une fonction de θ, dérivable, avec pour tout réel θ : f(θ) = θ2(1 + cos(θ)) + 4(1 − θ sin(θ) − cos(θ)) f′(θ) = 2θ(1 + cos(θ)) − θ2 sin(θ) − 4(sin(θ) + θ cos(θ) − sin(θ) = θ(2 − 2 cos(θ) − θ sin(θ)).
La fonction g : θ ↦ 2 − 2 cos(θ) − θ sin(θ) est elle-même dérivable et pour tout réel θ : g′(θ) = 3 sin(θ) − θ cos(θ), g″(θ) = 2 cos(θ) + θ sin(θ).
Dès lors, on obtient rapidement par signe des fonctions sinus et cosinus que la dérivée seconde g″ est positive sur [0, π/2] donc g′ est croissante sur cet intervalle, avec g′(0) = 0 donc g′ est positive sur [0, π/2].
De même, par signe des fonctions sinus et cosinus, la dérivée g′ est positive sur [π/2, π].
Sur l’intervalle [π, 3π/2], la dérivée seconde g″ est négative donc g′ est décroissante avec g′(π) = π et g′(3π/2) = −3 donc par continuité de g′ le théorème des valeurs intermédiaires assure qu’il existe un réel β ∈ ]π, 3π/2[ tel que g′(β) = 0, et la dérivée g′ reste positive sur [π, β], négative sur [β, 3π/2].
Enfin, par signe des fonctions sinus et cosinus, la dérivée g′ est négative sur l’intervalle [3π/2, 2π].
Finalement, on trouve que la fonction g est croissante sur [0, β] et décroissante sur [β, 2π] avec g(0) = g(2π) = 0, donc la fonction g est positive sur tout l’intervalle [0, 2π], donc la fonction f est croissante sur cet intervalle, avec f(0) = 0, ce qui justifie que f est positive sur l’intervalle [0, 2π] et achève de démontrer l’inégalité voulue.
| θ | 0 | π/2 | π | β | 3π/2 | 2π | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| g″(θ) | + | | | | | − | − | | | |||||
| g′(θ) | 0 | ↗ | 3 | + | π | ↘ | 0 | ↘ | −3 | − | |
| g(θ) | 0 | ↗ | ↗ | ↗ | g(β) | ↘ | ↘ | 0 | |||
| f′(θ) | 0 | + | + | + | + | + | |||||
| f(θ) | 0 | ↗ | ↗ | ↗ | ↗ | ↗ |
