Suite à une question d’un lecteur, j’ai récupéré le contenu d’une page que j’avais écrite en 2013 en marge de mon cours sur l’estimation. Il s’agit d’estimer les bornes d’une loi uniforme à partir d’un échantillon de n variables aléatoires indépendantes suivant cette loi.
À borne inférieure fixée
Lorsque la borne inférieure est connue, l’estimation de la borne supérieure est bien documentée.
Cas discret
Soit b ∈ N∗. On considère une famille de variables aléatoires indépendantes et identiquement distribuées (IID) (U1, …, Un) de loi uniforme sur l’ensemble ⟦1, b⟧, puis on définit la variable aléatoire M = max(U1, …, Un). Pour tout m ∈ ⟦1, b⟧ on a P(M = m) = P(M ≤ m) − P(M ≤ m − 1) = (mn − (m − 1)n)bn.
Si on remplace le paramètre b par une variable aléatoire B discrète dans N∗ avec les mêmes hypothèses que ci-dessus, c’est-à-dire PB = b(U1 = u1, …, Un = un) = 1bn, alors on montre la loi conditionnelle de B par rapport à (U1, …, Un) ne dépend que de M = max(U1, …, Un) :
On cherche donc une suite (βm) telle que pour tout b ∈ N∗, la variable aléatoire βM produise un estimateur sans biais de b.
Pour tout b ∈ N∗, on a l’équivalence b = E(βM) ⇔ ∑m = 1b βm × (mn − (m − 1)n) = bn+1.
Donc par différences des termes successifs on obtient la relation équivalente ∀m ∈ N∗, βm × (mn − (m − 1)n) = mn+1 − (m − 1)n+1.
Finalement, on obtient un estimateur sans biais du paramètre b de la loi uniforme à partir du maximum M de l’échantillon par (Mn+1 − (M − 1)n+1)(Mn − (M − 1)n).
Cas continu
Soit b ∈ R∗+. On considère une famille de variables aléatoires indépendantes et identiquement distribuées (U1, …, Un) de loi uniforme sur l’ensemble [0, b], puis on définit la variable aléatoire M = max(U1, …, Un). Pour tout m ∈ [0, b] on a P(M ≤ m) = mnbn donc la variable M suit une loi de densité x ↦ nxn−1bn.
Notons β une fonction de R∗+ dans lui-même et on résout par équivalences ∀b ∈ R∗+, b = ∫0b β(x) nxn−1bndx ⇔ ∀b ∈ R∗+, bn+1 = ∫0b β(x) × nxn−1dx autrement dit par dérivation ∀x ∈ R∗+, (n + 1)xn = β(x) × nxn−1.
Finalement, la fonction β est définie par ∀x ∈ R∗+, β(x) = (n+1)n x.
Estimation conjointe des bornes
Cette fois, la probabilité que toutes les variables Ui, indépendantes et identiquement distribuées de loi uniforme sur l’intervalle [a, b], se trouvent entre deux valeurs l et m s’écrit P(∀i, l ≤ Ui ≤ m) = (m − l)n(b − a)n.
Donc la fonction de densité associée au couple (L, M) = (min(U1, …, Un), max(U1, …, Un)) est définie par (x, y) ↦ −∂2∂x ∂y (y − x)n(b − a)n = n(n − 1)(y − x)n−2(b − a)n définie sur le demi-carré Δ de sommets (a, a), (a, b), (b, b).
Estimateurs ponctuels
On résout donc par équivalences : ∀(a, b) ∈ (R∗+)2, b = ∬Δ β(x, y) n(n − 1) (y − x)n−2(b − a)n dx dy ⇔ ∀(a, b) ∈ (R∗+)2, b(b − a)n = ∫ab∫ay β(x, y) n(n − 1) (y − x)n−2 dx dy d’où par dérivation par b puis par a, ∀(x, y) ∈ (R∗+)2, n(y − x)n−2(ny − x) = β(x, y) n(n − 1)(y − x)n−2 ⇔ ∀(x, y) ∈ (R∗+)2, β(x, y) = (ny − x)(n − 1).
Donc un estimateur sans biais de la borne supérieure de l’intervalle est défini par B = (nM − L)(n − 1) = M + (M − L)(n − 1). De même, un estimateur sans biais de la borne inférieure s’écrira A = L + (L − M)(n − 1).
La loi du couple (A, B) s’obtient assez facilement à partir de celle du couple (L, M) du fait de l’isomorphisme linéaire φ : (x, y) ↦ 1(n−1)(nx − y, ny − x) de jacobien |Jφ| = (n2 − 1)(n − 1)2 = (n + 1)(n − 1) et de réciproque φ−1(x, y) = 1(n+1)(nx + y, ny + x), par : f(A,B)(x, y) = (n(n − 1)n(y − x)n−2((n+1)n−1(b − a)n). Mais le support de ce couple n’est pas le triangle Δ défini plus haut. Il s’agit du triangle légèrement plus grand de sommets (a, a), (b, b), ((na−b)(n−1), (nb−a)(n−1)). On trouve que les deux côtés en dehors de la première bissectrice sont portés par les droites d’équations y = n(a − x) + a et y = (b−x)n + b.
Les lois marginales de A et de B s’obtiennent alors en intégrant la loi du couple le long des segments respectivement verticaux et horizontaux. La variable A admet donc comme support l’intervalle [(na−b)(n−1), b] et sa densité admet deux expressions différentes : pour tout x ≥ a, fA(x) = ∫x(b−x)n+b f(A,B)(x, y) dy = ((n − 1)n−1(b − x)n−1(nn−2(b − a)n) tandis que pour tout x < a, fA(x) = ∫n(a−x)+a(b−x)n+b f(A,B)(x, y) dy = ((n − 1)n−1(b − x)n−1(nn−2(b − a)n) − (n(n − 1)n−1(a − x)n−1(b − a)n = ((n − 1)n−1((b − x)n−1 − nn−1(a − x)n−1))(nn−2(b − a)n).

Cette fonction de densité est continue, de classe (n−2) sur l’intérieur du support et en b, avec un maximum en (n(n−1)(n−2)a − b)(n(n−1)(n−2) − 1).
De même, la variable B admet pour support l’intervalle [a, (nb−a)(n−1)] et sa densité admet deux expressions différentes : pour tout y ≤ b, fB(y) = ((n − 1)n−1(y − a)n−1(nn−2(b − a)n) tandis que pour tout y > b, fB(y) = ((n − 1)n−1((y − a)n−1 − nn−1(y − b)n−1))(nn−2(b − a)n) qui admet un maximum en (n(n−1)(n−2)b − a)(n(n−1)(n−2) − 1).
Intervalles de confiance
Il est tentant de chercher des intervalles de confiance centrés sur les meilleurs estimateurs ponctuels calculés précédemment, mais la fonction de densité du maximum en la valeur du paramètre s’écrit fM(b) = n(b − a) tandis que la fonction de densité de l’estimateur sans biais s’évalue à fB(b) = n(1 − 1n)n(b − a) ∼n→+∞ n(e (b − a)). On obtiendrait donc des intervalles deux à trois fois moins précis pour le même niveau de confiance.
Il est même possible qu’un intervalle de confiance ne contienne pas l’estimateur sans biais. En effet, ce dernier minimise le risque quadratique et donc tient compte des valeurs extrêmes, tandis que l’intervalle de confiance assure simplement une probabilité de présence sur un intervalle réduit, et peu importe si des valeurs rares sont très éloignées.
Si l’on souhaite un intervalle de confiance pour chacune des deux bornes avec un niveau de confiance global, il ne suffit pas que chacun des intervalles soit défini avec ce niveau de confiance, car les risques se cumulent (et de façon sous-additive). Ainsi, pour un niveau de risque α, on cherche deux réels positifs δ et δ′ tels que P(a ∈ [L − δ, L] et b ∈ [M, M + δ′]) = 1 − α.
Par symétrie, on impose δ = δ′. Par invariance par translation, cette amplitude ne dépend (pour α fixé) que de la différence M − L. Enfin, par homogénéité, cette dépendance est linéaire.
On calcule donc P(a ∈ [L − k(M − L), L] et b ∈ [M, M + k(M − L)]), ce qui revient à intégrer la fonction de densité du couple (L, M) sur le quadrilatère défini par les inégalités x ≥ a, y ≤ b, y ≥ (x − a)k + x, y ≥ (b + kx)(1 + k). Il s’agit d’un quadrilatère convexe et symétrique par rapport à la droite d’équation y = a + b − x. Cette même symétrie laisse invariante la fonction de densité du couple (L, M), donc il suffit d’intégrer sur le triangle de sommets (a, b), (a, (b+ka)(1+k)), (((1+k)a+kb)(1+2k), ((1+k)b+ka)(1+2k)).
Donc la probabilité définie plus haut s’écrit gn(k) = 1 + 1(1+2k)n−1 − 2(1+k)n−1 et correspond à la fonction de répartition de la variable Yn = max((L−a)(M−L), (b−M)(M−L)).
Il est facile de tabuler la fonction gn pour définir des intervalles de confiance. Pour des niveaux de risque faibles, on peut même négliger le deuxième terme, d’où l’approximation k ≈ n−1√(2α) − 1. À titre d’exemple, pour un niveau de confiance de 90 % avec un échantillon de taille n = 10, on trouve k ≈ 0,39, ce qui revient à élargir l’intervalle observé d’un tiers à chaque extrémité.
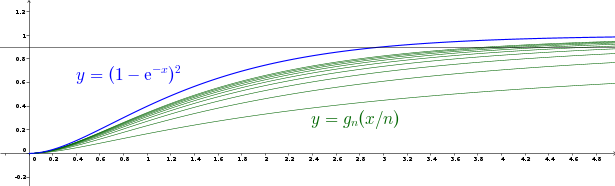
La suite des variables nYn converge en loi vers une variable Z de fonction de répartition FZ(t) = limn→+∞gn(tn) = 1 + e−2t − 2 e−t = (1 − e−t)2 ce qui permet d’obtenir une approximation des quantiles lorsque n est grand, mais la convergence est relativement lente.
Domaine de confiance de surface minimale
Au lieu de chercher un intervalle de confiance pour chaque borne, on peut chercher un domaine de confiance pour le couple (a, b), à l’intérieur du quart de plan délimité par les inéquations x ≤ L et y ≥ M. Cette zone constitue le premier quadrant d’un repère orthogonal d’unité M−L, dans lequel le point (a, b) a pour coordonnées ((L−a)(M−L), (b−M)(M−L)).
Or la loi de ce couple de variables aléatoires s’obtient facilement par le difféomorphisme ψ : (x, y) ↦ ((x−a)(y−x), (b−y)(y−x)) de jacobienne Jψ = 1(y − x)2 | y−a, a−x ; b−y, x−b | et de réciproque ψ−1(x, y) = 1(1+x+y) (ay + (1 + x)b, (1 + y)a + xb), donc on lui trouve une densité : f(S,T)(x, y) = (n(n − 1))(1 + x + y)n+1.
Le domaine de confiance de surface minimale pour (a, b) correspond alors au domaine de fluctuation de surface minimale pour (S, T). Comme le gradient de la fonction de densité est positivement colinéaire au vecteur (−1, −1), ce domaine est un triangle isocèle rectangle délimité dans le quart de plan par une ligne de niveau x + y = c. La probabilité associée s’écrit alors :
Cette probabilité décrit également la fonction de répartition du ratio de l’excédent de la largeur de l’intervalle sur l’amplitude observée F(b−a)(M−L)−1(c).
